딥넷트웍 학습 시키기 (backpropagation)
May 19, 2019
해당 게시물은 Edwith에서 제공하는
머신러닝과 딥러닝 BASIC을 듣고 요약 정리한 글입니다.
Neural Network (NN)
두개의 유닛의 Weight과 Bias를 학습시키는 방법
Gradient descent알고리즘을 사용
정의된 Cost함수의 그래프에서 하나의 점에서
값을 미분해 기울기를 구하며 그래프의 최저점까지 내려가면서 값을 구한다.
Back propagation
예측값과 실제값을 비교해 Cost값을 뒤에서 부터 앞으로
이동하면서 미분값과 어떤 값을 조정해야하는지 계산하는 알고리즘
Back Propagation 예제
위의 식을 그래프(NN) 형태의 그림으로 표현하면 아래와 같다.
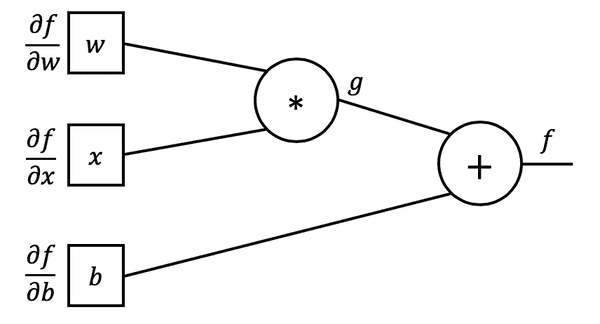
위의 그림으로 , , 가 에 미치는 영향을
구하기위해 미분값을 계산해 사용해야한다.
-
forward ()
- 실제 존재하는 학습값으로 계산
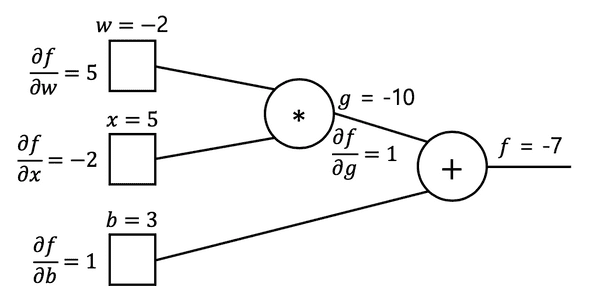
가 에 미치는 영향은 로 1이다.
가 에 미치는 영향은 로 1이다.
가 에 미치는 영향은 로 -2다.
가 에 미치는 영향은 로 5다.
여기에서 미분값의 의미는 의 값은 1인데 이것은 의 영향이
1:1과 같다는 뜻이고 d의 값은 5인데 이것은 의 영향이
5:1과 같다는 뜻이다. 의 값이 1만큼 변하면 의 값 5배 바뀐다는 의미다.
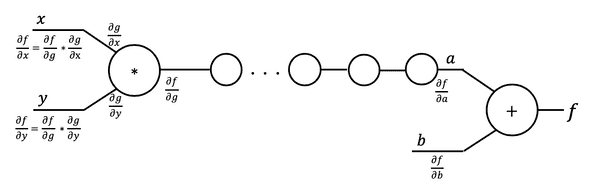
여러개의 Layer가 겹쳐있어도 위와 같은 그림의 방법을 사용하면 된다.
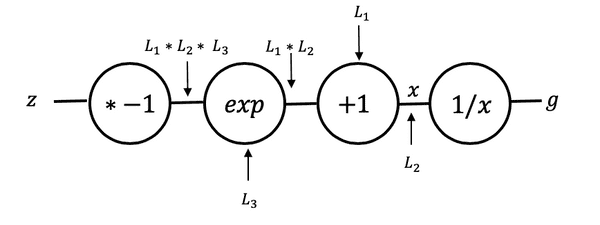
Sigmoid의 그래프 표현
위의 Sigmoid Function을 아래와 같은 그래프로 표현되어
Backpropagation을 계산할 수 있다.
Tensorflow 코드로 구현
TensorFlow또한 모든 것을 그래프로 가지고 계산한다.
hypothesis = tf.sigmoid(tf.matmul(L2, W2) + b2)
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) * tf.log(1 - hypothesis))