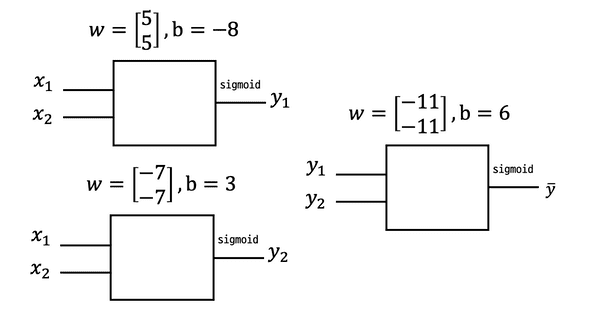해당 게시물은 Edwith에서 제공하는
머신러닝과 딥러닝 BASIC을 듣고 요약 정리한 글입니다.
Neural Network를 사용해 XOR 풀기
| X1 |
X2 |
XOR |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
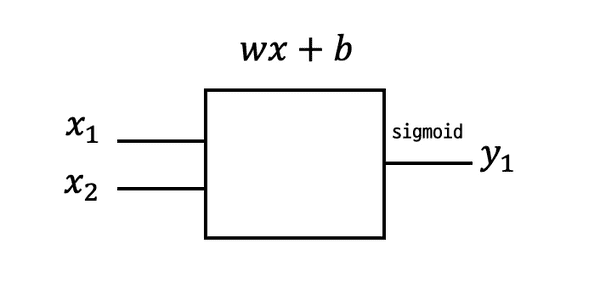
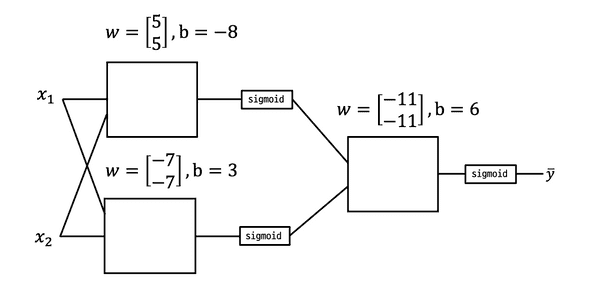
하나의 Unit
위의 Unit과 같은 모양이지만 다른 weight과 bias를 갖는
두개의 Unit에서 나온 결과(Y1, Y2) 다른 Unit에 넣어 값을 예측한다.
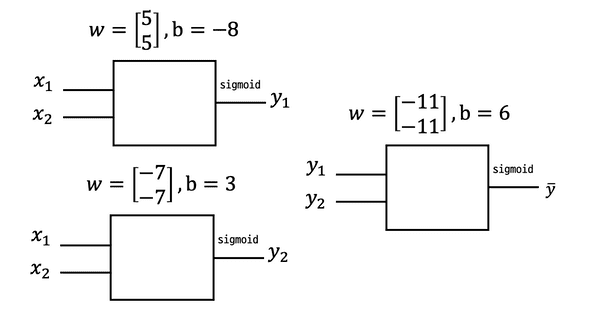
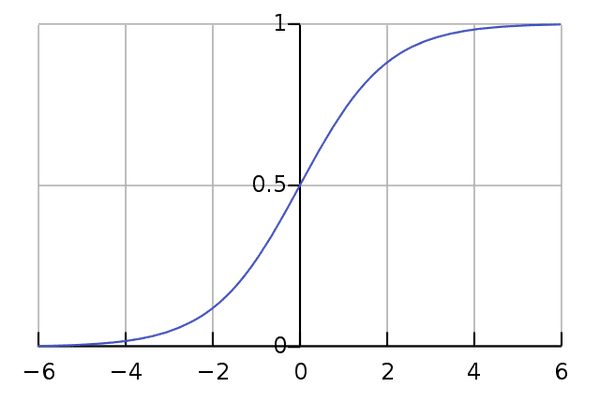
Sigmoid Function
입력값이 작을수록 0에 수렴
입력값이 클수록 1에 수렴
[이미지 참조]
계산 과정
Y1=[00][55]−8=−8,Sigmoid(Y1)=0
Y2=[00][−7−7]+3=3,Sigmoid(Y2)=1
Yˉ=[01][−11−11]+6=−11+6=5,Sigmoid(Yˉ)=0
위와 같은 방법으로 아래의 모든 케이스를 진행
결과 확인 표
| X1 |
X2 |
Y1 |
S(Y1) |
Y2 |
S(Y2) |
Ȳ |
S(Ȳ) |
XOR |
| 0 |
0 |
-8 |
0 |
3 |
1 |
-5 |
0 |
0 |
| 0 |
1 |
-3 |
0 |
-4 |
0 |
6 |
1 |
1 |
| 1 |
0 |
-3 |
0 |
-4 |
0 |
6 |
1 |
1 |
| 1 |
1 |
2 |
1 |
-11 |
0 |
-5 |
0 |
0 |
위의 표를 확인하면 2개의 Unit과 Sigmoid Function을
사용한 결과 XOR문제가 해결되었다.
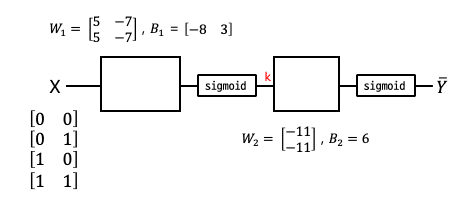
Forward Propagation
아래와 같은 구조를 하나의 Neural Network라고 할 수 있다.
다른 weight값과 bias값은 존재 가능
위의 구조는 아래의 Nominal Classification과 비슷하다.
⎣⎡wA1wB1wC1wA2wB2wC2wA3wB3wC3⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡wA1x1wB1x1wC1x1wA2x2wB2x2wC2x2wA3x3wB3x3wC3x3⎦⎤=⎣⎡yAyByC⎦⎤
그림으로 위의 그림의 구조를 표현해보자면
다음과 같은 구조로 표현이 가능하다.
위의 구조를 수식으로 정리하면 아래와 같다.
뒤쪽 Unit 구조의 수식화
K(X)=Sigmoid(XW1+B1)
모든 Unit 구조의 수식화
Yˉ=H(X)=Sigmoid(K(X)W2+B2)
다음 수식을 코드로 구현하면 아래와 같다.
K = tf.sigmoid(tf.matmul(X,, W1) + b1)
hypothesis = tf.sigmoid(tf.matmul(K, W2) + 2)