fp-ts로 Typescript 함수형 프로그래밍 시작하기 8 (Monad)
June 05, 2021
본 포스트는 fp-ts 공식 문서의 Learning Resources에 있는 Getting Started에서 소개하는 문서들을 번역하며 학습한 문서입니다. 원본 문서는 링크에서 확인할 수 있으며 작성한 코드들은 여기에서 확인할 수 있습니다.
fp-ts 시작하기 (Monad)
지난 포스트에서 우리는 M이 Applicative 인스턴스를 인정한다면 g를 들어 올림으로써 순수한 n항 프로그램 g로 이펙트 있는 프로그램 f: (a: A) => M<B>를 구성할 수 있음을 보았습니다.
| 프로그램 f | 프로그램 g | 조합 |
|---|---|---|
| 순수한 | 순수한 | g ∘ f |
| 이펙트 있는 | 순수한, n항 |
liftAn(g) ∘ f |
그러나 마지막 한 가지 경우를 해결해야 합니다. 두 프로그램이 모두 이펙트가 있다면 어떻게 할 수 있을까요?
f: (a: A) => M<B>
g: (b: B) => M<C>그런 f와 g의 “조합”은 무엇일까요?
이 마지막 경우를 처리하기 위해서는 중첩된 컨텍스트로 끝나기 쉽기 때문에 Functor보다 더 강력한 것이 필요합니다.
문제: 중첩된 컨텍스트
더 많은 것이 필요한 이유를 더 잘 설명하기 위해 몇 가지 예시를 살펴보겠습니다.
예시 (M = Array)
트위터 사용자의 팔로워를 검색하고 싶다고 가정해 보겠습니다.
interface User {
followers: Array<User>;
}
const getFollowers = (user: User): Array<User> => user.followers;
const followersOfFollowers = (user: User): Array<Array<User>> =>
getFollowers(user).map(getFollowers);뭔가 잘못된 것이 있습니다. followersOfFollowers 함수의 반환 타입은 Array<Array<User>>이지만 우리는 Array<User> 타입을 반환하기를 원합니다.
우리는 중첩된 배열을 평평하게 만들어야 합니다.
fp-ts에서 제공하는 flatten: <A>(mma: Array<Array<A>>) => Array<A> 함수를 사용하면 편리합니다.
import { flatten } from 'fp-ts/lib/Array';
const followersOfFollowers = (user: User): Array<User> =>
flatten(getFollowers(user).map(getFollowers));좋습니다. 다른 데이터 구조는 어떨까요?
예시 (M = Option)
숫자 목록의 가장 앞의 데이터의 역수를 계산하고 싶다고 가정해 보겠습니다.
import { Option, some, none, option } from 'fp-ts/lib/Option';
import { head } from 'fp-ts/lib/Array';
const inverse = (n: number): Option<number> => (n === 0 ? none : some(1 / n));
const inverseHead = (arr: Array<number>): Option<Option<number>> =>
option.map(head(arr), inverse);다시 한번 발생했습니다. inverseHead 함수는 Option<Option<number>> 타입을 반환하고 있지만 우리는 Option<number> 타입이 반환되기를 원합니다.
우리는 중첩된 Option을 평평하게 만들어야 합니다.
import { isNone } from 'fp-ts/lib/Option';
const flatten = <A>(mma: Option<Option<A>>): Option<A> =>
isNone(mma) ? none : mma.value;
const inverseHead = (arr: Array<number>): Option<number> =>
flatten(option.map(head(arr), inverse));모든 flatten 함수들은 우연히 생긴 것이 아닙니다. 이것들은 모두 안에 함수형적인 패턴이 존재합니다.
실제로 이러한 모든 타입 생성자(및 기타 많은 생성자)는 Monad 인스턴스를 허용하고 있습니다.
flatten은 Monad의 가장 고유한 기능입니다.
그래서 Monad는 무엇인가요?
아래 내용이 Monad가 자주 제시되는 방식입니다.
정의
Monad는 아래와 같이 세 가지로 정의됩니다.
(1) Functor 인스턴스를 허용하는 타입 생성자 M
(2) 아래의 시그니처를 갖는 of 함수
of: <A>(a: A) => HKT<M, A>(3) 아래 시그니처를 갖는 flatMap 함수
flatMap: <A, B>(f: (a: A) => HKT<M, B>) => ((ma: HKT<M, A>) => HKT<M, B>)
HKT타입은 제네릭 타입 생성자를 나타내는fp-ts방식이며HKT<M, X>는 타입X에 적용된 타입 생성자M(즉,M<X>)을 생각할 수 있습니다.
of와 flatMap 함수는 아래의 세 가지 조건을 만족해야 합니다.
- 왼쪽 항등식(Left identity):
flatMap(of) ∘ f = f - 오른쪽 항등식(Right identity):
flatMap(f) ∘ of = f - 결합 법칙(Associativity):
flatMap(h) ∘ (flatMap(g) ∘ f) = flatMap((flatMap(h) ∘ g)) ∘ f
여기서 f, g, h는 모두 이펙트가 있는 함수이고 ∘는 일반적인 함수 조합입니다.
좋습니다. 그런데 왜?
이런 정의를 처음 보았을 때 첫 반응은 당황했습니다.
아래의 모든 질문이 내 머릿속에서 맴돌고 있었습니다.
- 왜 그 두 가지 특정한 기능을 하고 왜 그런 타입을 갖고 있나요?
- 왜 이름이 “flatMap”일까요?
- 왜 규칙들이 있고 그것들은 무엇을 의미할까요?
- 하지만 무엇보다도
flatten은 어디에 있을까요?
이 포스트에서는 각 질문에 대한 답변을 시도합니다.
문제로 돌아가 보겠습니다. 두 개의 이펙트 있는 함수(Kleisli arrows라고도 함)의 조합은 무엇입니까?
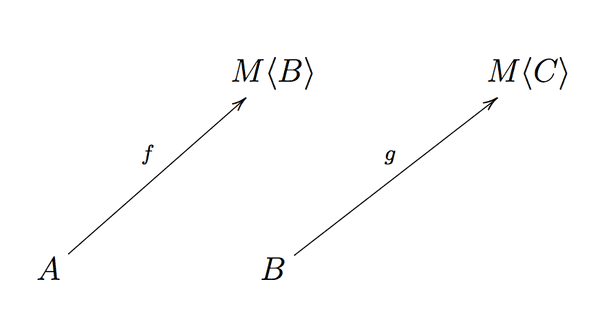
나는 그것의 타입이 무엇인지조차 모릅니다.
잠깐… 우리는 이미 조합에 관한 추상화를 만났습니다. 카테고리에 관해 얘기한 것을 기억하고 있습니까?
카테고리는 조합의 본질을 포착합니다.
우리는 이 문제를 카테고리 문제로 바꿀 수 있습니다. Kleisli arrows의 조합 모델에 맞는 카테고리를 찾을 수 있습니까?
Kleisli 카테고리
이펙트 있는 함수만 포함하는 카테고리 K (Kleisli 카테고리)를 구성해 보겠습니다.
- 객체는 TS 카테고리와 동일한 객체로 즉 모든 TypeScript 타입입니다.
- 형태는 아래와 같이 구성됩니다. TS에 Kleisli 화살표
f: A ⟼ M<B>가 있으면 K에서 화살표f': A ⟼ B를 그립니다.
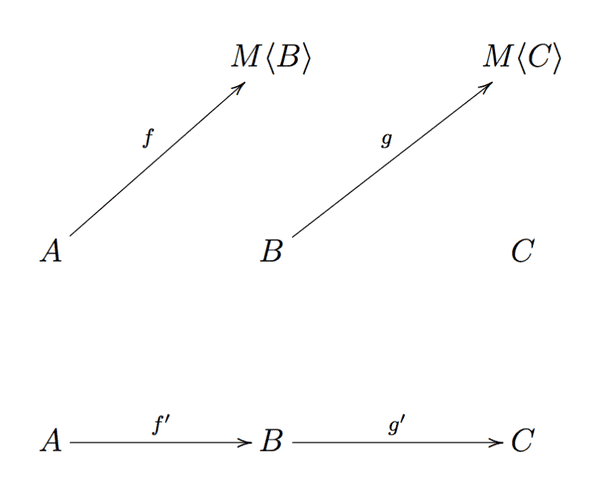
그렇다면 K에서 f'와 g'의 조합은 아래 이미지에서 h'라고 표시된 점선 화살표입니다.
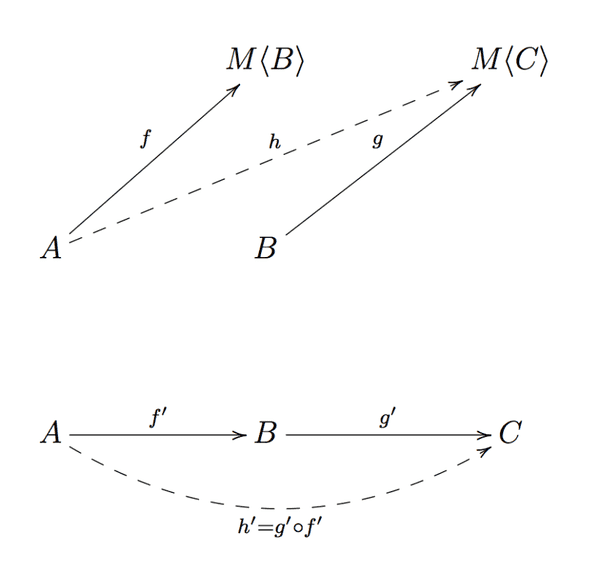
h'는 A에서 C로 이동하는 화살표이므로 TS에는 A에서 M<C>까지에 해당하는 함수 h가 있어야 합니다.
따라서 TS에서 f와 g의 조합에 대한 좋은 후보는 여전히 (a: A) => M <C>의 시그니처를 가진 이펙트 있는 함수입니다.
그러한 함수를 어떻게 구성 할 수 있을까요?
우리는 단계별로 조합을 구성합니다.
Monad 정의의 요점(1)은 M이 Functor 인스턴스를 허용하므로 함수 g: (b: B) => M<C>를 함수 lift(g): (mb: M<B>) => M<M<C>>로 들어 올릴 수 있습니다. (여기서는 동의어 map을 사용하고 있습니다.)
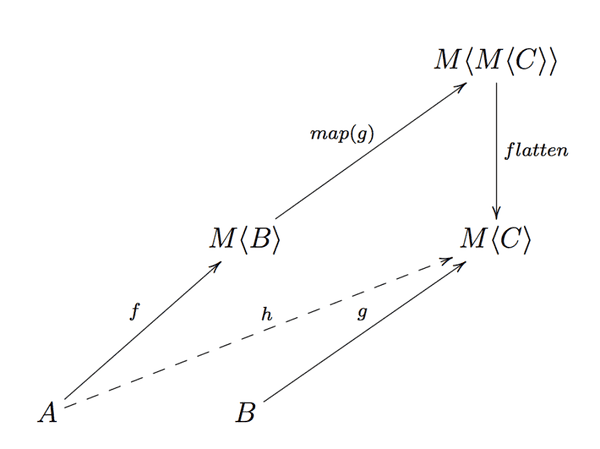
flatMap은 여기서 유래된다.
그리고 이제 우리는 막혔습니다. M<M<C>> 타입의 값을 M<C> 타입의 값으로 평평하게 만들 수 있는 Functor 인스턴스에 대한 기능이 없습니다. 추가적인 flatten 기능이 필요합니다.
이러한 기능을 정의 할 수 있다면 찾고 있는 조합을 얻을 수 있습니다.
h = flatten ∘ map(g) ∘ f
하지만 flatten ∘ map(g)은 flatMap입니다. 이름은 여기에서 유래되었습니다!
h = flatMap(g) ∘ f
이제 “조합표”를 업데이트 할 수 있습니다.
| 프로그램 f | 프로그램 g | 조합 |
|---|---|---|
| 순수한 | 순수한 | g ∘ f |
| 이펙트 있는 | 순수한, n항 |
liftAn(g) ∘ f |
| 이펙트 있는 | 이펙트 있는 | flatMap(g) ∘ f |
of는 어떤가요? of는 K의 항등성 형태에서 유래됩니다. K의 각 항등성 형태에 대해 A에서 M<A>까지에 해당하는 함수가 있어야 합니다 (즉, of: <A>(a: A) => M<A>)
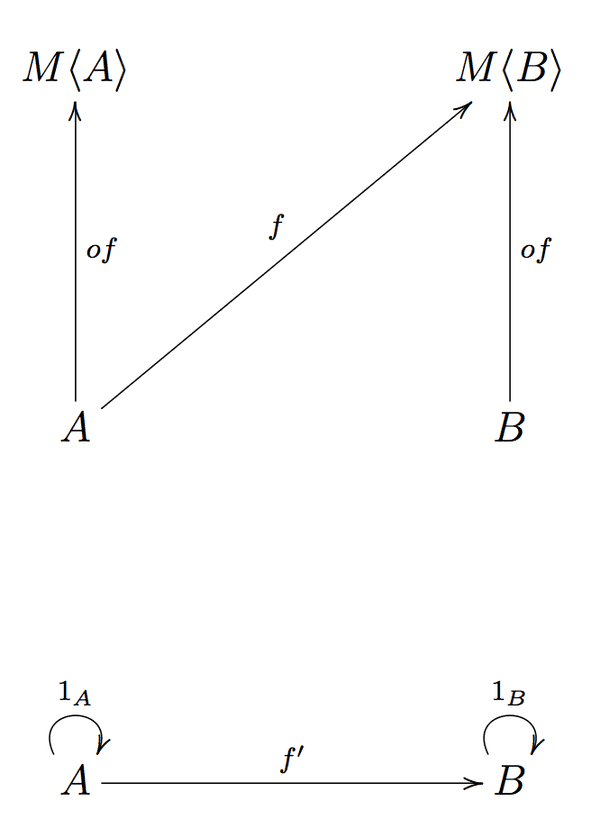
of는 여기서 유래된다.
법칙
마지막 질문: 법칙은 어디에서 왔습니까? 그것들은 TS로 번역된 K의 카테고리 법칙일 뿐입니다.
| 법칙 | K | TS |
|---|---|---|
| 왼쪽 항등식 (Left identity) | 1B ∘ f’ = f’ |
flatMap(of) ∘ f = f |
| 오른쪽 항등식 (Right identity) | f' ∘ 1A = f' |
flatMap(f) ∘ of = f |
| 결합 법칙 (Associativity ) | h' ∘ (g' ∘ f') = (h' ∘ g') ∘ f' |
flatMap(h) ∘ (flatMap(g) ∘ f) = flatMap((flatMap(h) ∘ g)) ∘ f |
fp-ts의 Monad
fp-ts에서 flatMap 함수는 chain이라는 변형에 의해 모델링 되며, 기본적으로 인수가 재배열 된 flatMap 입니다.
flatMap: <A, B>(f: (a: A) => HKT<M, B>) => ((ma: HKT<M, A>) => HKT<M, B>)
chain: <A, B>(ma: HKT<M, A>, f: (a: A) => HKT<M, B>) => HKT<M, B>참고:
chain은flatMap에서 파생될 수 있으며 반대도 가능하다.
이제 중첩된 컨텍스트의 문제를 보여주는 예제로 돌아가 chain을 사용하여 문제를 해결할 수 있습니다.
원문에서는
Option.chain과Array의chain을 사용하라고 작성되어 있지만, 최신 버전의 fp-ts에서는 deprecated 되어 있으며arrayChain과optionChain을 사용하면 됩니다.
import type { Option } from 'fp-ts/lib/Option';
import { chain as arrayChain, head } from 'fp-ts/lib/Array';
import { chain as optionChain } from 'fp-ts/lib/Option';
const followersOfFollowers = (user: User): Array<User> =>
arrayChain(getFollowers)(getFollowers(user));
const headInverse = (arr: Array<number>): Option<number> =>
optionChain(inverse)(head(arr));결론
함수형 프로그래밍은 이펙트로 함수를 조합하는 보편적인 방법을 제공합니다. Functor, Applicative Functor 및 Monad는 모두 다른 종류의 프로그램을 조합하기 위한 원칙적인 도구를 제공하는 추상화입니다.
요약 : 함수형 프로그래밍은 실제로 조합에 관한 것입니다.
