fp-ts로 Typescript 함수형 프로그래밍 시작하기 6 (Functor)
May 02, 2021
본 포스트는 fp-ts 공식 문서의 Learning Resources에 있는 Getting Started에서 소개하는 문서들을 번역하며 학습한 문서입니다. 원본 문서는 링크에서 확인할 수 있으며 작성한 코드들은 여기에서 확인할 수 있습니다.
fp-ts 시작하기 (Functor)
카테고리에 대한 지난 포스트에서 TS 카테고리 (TypeScript 카테고리)와 함수 조합의 핵심 문제를 제시했습니다.
두 가지 일반 함수
f: (a: A) => B와g: (c: C) => D를 어떻게 조합할 수 있을까요?
이 문제에 대한 해결책을 찾는 것이 왜 그렇게 중요할까요?
왜냐하면 카테고리가 프로그래밍 언어를 모델링하는 데 사용될 수 있다면, 형태(즉, TS의 함수)는 프로그램을 모델링하는 데 사용될 수 있기 때문입니다.
따라서 문제를 해결하는 것은 일반적인 방식으로 프로그램을 조합하는 방법을 찾는 것을 의미하기도 합니다. 그리고 이것은 개발자에게 꽤 흥미롭지 않을까요?
프로그램으로서의 함수
순수 프로그램을 다음과 같은 시그니처를 가진 함수라고 부릅니다.
(a: A) => B;이 시그니처는 A 타입의 입력을 받고 이펙트 없이 타입 B의 결과를 생성하는 프로그램 모델입니다.
이펙트 있는 프로그램을 아래와 같은 시그니처를 가진 함수라고 부릅니다.
(a: A) => F<B>이 시그니처는 A타입 입력을 받고 이펙트 F와 함께 유형 B의 결과를 생성하는 프로그램 모델입니다. 여기서 F는 타입 생성자입니다.
타입 생성자는 0개 이상의 타입 인자를 받고 다른 형식을 반환하는 n항 형식 연산자입니다.
예시
타입 string이 주어지면 Array 타입 생성자는 타입 Array<string>를 반환합니다.
여기서 우리는 n >= 1인 n항 생성자에 관심이 있습니다.
| 타입 생성자 | 이펙트 (해석) |
|---|---|
Array<A> |
비결정론적 연산 |
Option<A> |
실패할지도 모르는 연산 |
Task<A> |
비동기 연산 |
이제 아래 주요 문제로 돌아갈 수 있습니다.
두 가지 일반 함수
f: (a: A) => B와g: (c: C) => D를 어떻게 조합할 수 있을까요?
일반적인 문제는 다루기 어렵기 때문에 B와 C에 제약을 가할 필요가 있습니다.
우리는 이미 B = C이면 일반적인 함수 조합이 가능하다는 것을 정답으로 알고 있습니다.
function compose<A, B, C>(g: (b: B) => C, f: (a: A) => B): (a: A) => C {
return a => g(f(a));
}다른 경우는 어떻게 할 수 있을까요?
제약 조건 B = F<C>가 Functor로 연결되는 경우
B = F<C>의 일부 타입 생성자 F 또는 다른 말로 바꿔 아래와 같은 제약 조건을 고려해 볼 수 있습니다.
f: (a: A) => F<B>는 이펙트가 있는 프로그램입니다.g: (b: B) => C는 순수한 프로그램입니다.
f를 g로 조합하기 위해 함수 (b: B) => C에서 함수 (fb: F<B>) => F <C>로 g를 들어 올려(lift) 일반적인 함수 조합을 사용할 수 있습니다. (f의 반환 타입은 들어 올려진 함수의 입력 타입과 동일합니다)
원래의 문제를 다른 문제로 바꿨습니다. 그렇다면 그런 lift 함수를 찾을 수 있을까요?
몇 가지 예시를 살펴볼 수 있습니다.
예시 (F = Array)
function arrayLift<B, C>(g: (b: B) => C): (fb: Array<B>) => Array<C> {
return fb => fb.map(g);
}예시 (F = Option)
import type { Option } from 'fp-ts/lib/Option';
import { isNone, some, none } from 'fp-ts/lib/Option';
function lift<B, C>(g: (b: B) => C): (fb: Option<B>) => Option<C> {
return (fb) => (isNone(fb) ? none : some(g(fb.value)));
}예시 (F = Task)
import type { Task } from 'fp-ts/lib/Task';
function lift<B, C>(g: (b: B) => C): (fb: Task<B>) => Task<C> {
return (fb) => () => fb().then(g);
}모든 lift 함수는 거의 동일하게 보이지만 우연이 아닙니다. 모두 아래에 함수적인 패턴이 있습니다.
실제로 이러한 모든 타입 생성자(그리고 다른 많은 것들)는 Functor 인스턴스를 허용합니다.
Functor
Functor는 카테고리 구조를 보존하는 카테고리 간의 매핑입니다. 즉, 동일 형태와 조합을 보존합니다.
카테고리는 두 가지 (객체와 형태)로 구성되므로 Functor도 두 가지로 구성됩니다.
- C의 각 객체
X와 D의 객체와 관련된 객체 간의 매핑 - C의 각 형태와 D의 형태와 연관되는 형태 간의 매핑
여기서 C와 D는 두 가지 카테고리(일명 두 가지 프로그래밍 언어)입니다.
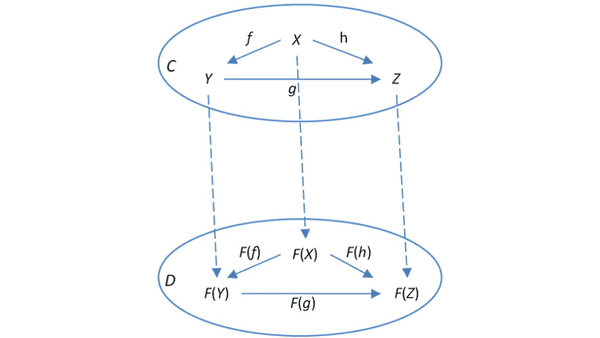
서로 다른 두 프로그래밍 언어 간의 매핑이 흥미로운 아이디어라고 해도 C와 D가 일치하는 매핑(TS와 함께)에 더 관심이 있습니다. 이 경우에는 endofunctor(“endo”는 “내부”, “내부”를 의미)에 대해 이야기합니다.
지금부터 Functor를 사용할 때에는 실제로 TS에서 endofunctor를 의미합니다.
정의
Functor는 (F, lift) 쌍입니다.
F는 각 타입X를 타입F<X>(객체 간 매핑)에 매핑하는n항 타입 생성자 (n >= 1)입니다.lift는 아래와 같은 시그니처가 있는 함수입니다.
lift: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)각 함수 f: (a: A) => B를 함수 lift(f): (fa: F<A>) => F<B> (형태 간 매핑)에 매핑합니다.
Functor는 아래와 같은 속성이 유지되어야 합니다.
lift(identityX)=identityF(X): Identity가 Identity에 매핑 되어야 한다.lift(g ∘ f)=lift(g) ∘ lift(f): 조합 매핑은 매핑의 조합이다.
lift 함수는 map이라는 변형으로도 알려져 있으며 기본적으로 lift는 인자가 재배치 되어있습니다.
lift: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)
map: <A, B>(fa: F<A>, f: (a: A) => B) => F<B>참고:
map은lift에서 파생될 수 있으며 반대도 마찬가지로 가능합니다.
fp-ts에서의 Functor
fp-ts에서 Functor 인스턴스를 어떻게 정의할 수 있을까요? 실제 예시를 확인해 볼 수 있습니다.
아래의 인터페이스 선언은 API 호출 응답 모델을 정의합니다.
interface Response<A> {
url: string;
status: number;
headers: Record<string, string>;
body: A;
}body 필드는 매개 변수화되어 있으므로 Response는 n >= 1인 n항 타입 생성자(필요한 전제 조건)이므로 Response가 Functor 인스턴스에 적합한 후보가 될 수 있습니다.
Response에 대한 Functor 인스턴스를 정의하려면 fp-ts에서 요구하는 일부 기술과 함께 map 함수를 정의해야 합니다.
import { Functor1 } from 'fp-ts/lib/Functor';
const URI = 'Response';
type URI = typeof URI;
declare module 'fp-ts/lib/HKT' {
interface URItoKind<A> {
Response: Response<A>;
}
}
interface Response<A> {
url: string;
status: number;
headers: Record<string, string>;
body: A;
}
function map<A, B>(fa: Response<A>, f: (a: A) => B): Response<B> {
return { ...fa, body: f(fa.body) };
}
// `Response`를 위한 Functor 인스턴스
export const functorResponse: Functor1<URI> = {
URI,
map,
};일반적인 문제가 해결되었을까요?
전혀 해결되지 않았습니다. Functor를 사용하면 순수 프로그램 g로 효과적인 프로그램 f를 구성할 수 있지만, g는 단항이어야 합니다. 즉, 입력으로 하나의 인자만 허용해야 합니다. g가 두 개 또는 세 개의 인수를 받아들이면 어떻게 할 수 있을까요?
| 프로그램 f | 프로그램 g | 조합 |
|---|---|---|
| 순수함 | 순수함 | g ∘ f |
| 이펙트가 있는 | 순수함(단항) | lift(g) ∘ f |
| 이펙트가 있는 | 순수한(n항, n > 1) |
? |
이러한 상황을 처리하기 위해서는 더 많은 것이 필요합니다. 다음 포스트에서는 함수형 프로그래밍의 또 다른 놀라운 추상화인 Applicative Fuctor에 대해 이야기할 것입니다.
요약 : 함수형 프로그래밍은 조합에 관한 것입니다.
