fp-ts로 Typescript 함수형 프로그래밍 시작하기 5 (Category)
May 01, 2021
본 포스트는 fp-ts 공식 문서의 Learning Resources에 있는 Getting Started에서 소개하는 문서들을 번역하며 학습한 문서입니다. 원본 문서는 링크에서 확인할 수 있으며 작성한 코드들은 여기에서 확인할 수 있습니다.
fp-ts 시작하기 (Category)
지난 포스트에서 우리는 함수형 프로그래밍에 사용되는 몇 가지 기본 추상화인 Eq, Ord, Semigroup과 Monoid를 보았습니다.
다음 포스트에서는 함수형 프로그래밍을 더욱더 흥미롭게 만드는 몇 가지 고급 추상화를 살펴볼 것입니다.
이야기적으로 fp-ts에 포함된 첫 번째 고급 추상화는 Functor지만, Functor에 관해 이야기하기 전에 Functor를 만들기 위해 필요한 카테고리에 대해 배울 필요가 있습니다.
함수형 프로그래밍의 초석은 조합입니다. 그러나 이것이 정확히 무엇을 의미할까요? 두 가지가 조합된다고 말할 수 있을까요? 그리고 그것이 언제 모든 것이 잘 조합된다고 말할 수 있을까요?
우리는 조합에 대한 공식적인 정의가 필요합니다. 그것이 카테고리에 관한 모든 것입니다.
카테고리는 조합의 본질을 포착합니다.
카테고리
카테고리의 정의는 약간 길기 때문에 두 부분으로 나눌 것입니다.
- 첫 번째는 기술적인 것입니다. (우선 조합 요소를 정의해야 합니다).
- 두 번째 부분에는 우리가 가장 관심을 갖는 내용인 조합 개념이 포함됩니다.
Part I (정의)
카테고리는 (Objects, Morphisms) 쌍입니다.
Objects는 객체 모음입니다.Morphisms은 객체 사이의 형태 (또는 화살표) 모음입니다.
참고: 여기에서 “객체”라는 용어는 OOP와는 아무 관련이 없습니다. 객체를 검사할 수없는 블랙박스 또는 Morphisms을 위한 보조 자리 표시자로 생각할 수 있습니다.
각 Morphisms f에는 소스 객체 A와 대상 객체 B가 있으며 A와 B는 Objects입니다.
우리는 f: A ⟼ B라고 쓰고 “f는 A에서 B로의 형태”라고 말합니다.
Part II (조합)
아래 속성을 유지해야 하는 “조합”이라는 작업 ∘가 있습니다.
- 형태의 조합(Composition of morphisms):
f: A ⟼ B및g: B ⟼ C가Morphisms에서 두 가지 형태이면 세 번째Morphisms인f와g의 조합인A ⟼ C형태의g ∘ f가 있어야 합니다. - 결합법칙(Associativity): 만약
f: A ⟼ B,g: B ⟼ C와h: C ⟼ D를 만족한다면h ∘ (g ∘ f) = (h ∘ g) ∘ f를 만족해야 합니다. - 항등성(Identity): 모든 객체
X에 대해X ⟼ X는X에 대한 항등성 형태라고 불립니다. 따라서 모든 형태f: A ⟼ X및 모든 형태g: X ⟼ B에 대해identity ∘ f = f및g ∘ identity = g를 만족해야 합니다.
예시
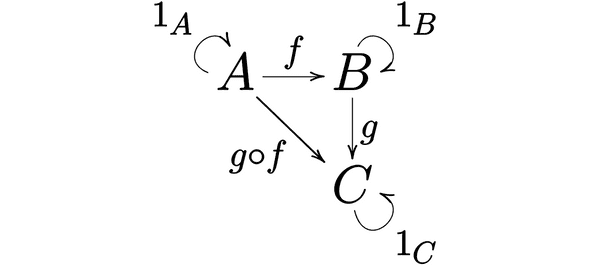
이 카테고리는 매우 간단합니다. 3개의 객체와 6개의 형태만 있습니다 (, , 는 A, B, C의 동일 형태입니다).
프로그래밍 언어로서의 카테고리
카테고리는 타입화 된 프로그래밍 언어의 단순화 된 모델로 해석될 수 있습니다.
- 객체는 타입입니다
- 형태는 함수입니다
∘는 일반적인 함수 조합입니다.
아래의 다이어그램은 단지 세 가지 타입과 작은 함수들이 있는 매우 단순한 가상의 프로그래밍 언어로 해석될 수 있습니다.
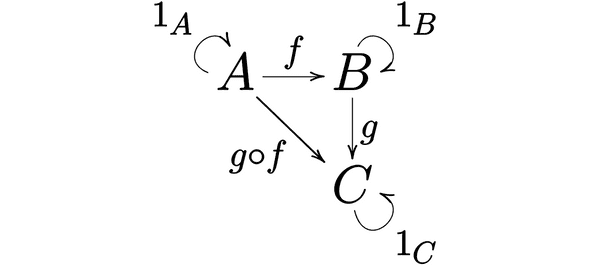
예를 들면 아래와 같습니다.
A = stringB = numberC = booleanf = string => numberg = number => booleang ∘ f = string => boolean
실제 구현은 아래와 같을 수 있습니다.
function f(s: string): number {
return s.length;
}
function g(n: number): boolean {
return n > 2;
}
// h = g ∘ f
function h(s: string): boolean {
return g(f(s));
}타입스크립트를 위한 카테고리
TypeScript 언어의 모델로 TS라는 이름을 갖는 카테고리를 정의 할 수 있습니다.
- 객체는 모든 TypeScript 타입입니다 :
string,number,Array<string>, … - 형태는 모든 TypeScript 함수입니다 :
(a: A) => B,(b: B) => C, … 여기서A,B,C, …는 TypeScript 타입입니다. - 동일 형태는 모두 단일 다형성 함수로 인코딩됩니다
const identity = <A>(a: A): A => a - 형태의 조합은 일반적인 연관된 함수 조합입니다.
TypeScript의 모델로서 TS는 너무 제한적으로 보일 수 있습니다. 반복문도, 조건문도, 거의 아무것도 사용하지 않습니다. 그런데도 이 단순화된 모델은 우리의 주요 목적인 잘 정의된 조합 개념에 대한 이유를 만족하기에 충분합니다.
조합의 핵심 문제
TS에서 우리는 두 가지 제네릭 함수 f: (a: A) => B 및 g: (c: C) => D를 B = C를 만족하는 경우에 조합할 수 있습니다.
function compose<A, B, C>(g: (b: B) => C, f: (a: A) => B): (a: A) => C {
return a => g(f(a));
}그러나 B != C이면 어떻게 할 수 있을까요? 이러한 함수를 어떻게 조합 할 수 있을까요? 포기해야 할까요?
다음 포스트에서는 어떤 조건에서 그러한 조합이 가능한지 살펴보며 Functor에 대해 이야기해보겠습니다.
