Minsu's Dev Log

Multinomial 개념 소개

해당 게시물은 Edwith에서 제공하는
머신러닝과 딥러닝 BASIC을 듣고 요약 정리한 글입니다.

Multinomial classificcation

Training Data

x1 (hours) x2 (attendance) y (grade)
10 5 A
9 5 A
3 2 B
2 4 B
11 1 C

x1, x2의 데이터로 y를 예측

X가 들어갔을 때 해당 데이터가 무슨 성적을 반환할지에 대한
3개의 독립적인 Classfier가 필요

1

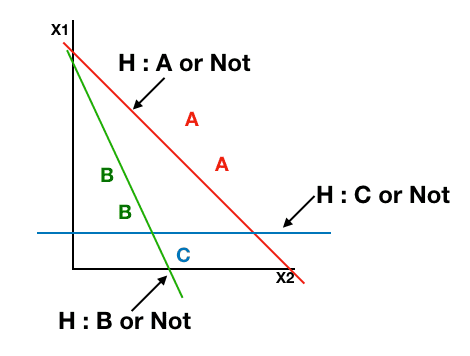
따라서 아래의 식이 3개 필요하다.

[w1w2w3][x1x2x3]=[w1x2+w2x2+w3x3] \begin{bmatrix} w_1 & w_2 & w_3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = [w_1x_2 + w_2x_2 + w_3x_3]

3개의 식을 독립적으로 계산하는 것은 복잡하기 때문에
하나의 행렬 곱셈식으로 합쳐서 이용

[wA1wA2wA3wB1wB2wB3wC1wC2wC3][x1x2x3]=[wA1x1wA2x2wA3x3wB1x1wB2x2wB3x3wC1x1wC2x2wC3x3]=[yA‾yB‾yC‾]=[HA(x)HB(x)HC(x)] \begin{bmatrix} w_{A1} & w_{A2} & w_{A3} \\ w_{B1} & w_{B2} & w_{B3} \\ w_{C1} & w_{C2} & w_{C3} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} w_{A1}x_1 & w_{A2}x_2 & w_{A3}x_3 \\ w_{B1}x_1 & w_{B2}x_2 & w_{B3}x_3 \\ w_{C1}x_1 & w_{C2}x_2 & w_{C3}x_3 \\ \end{bmatrix} = \begin{bmatrix} \overline{y_A} \\ \overline{y_B} \\ \overline{y_C} \\ \end{bmatrix} = \begin{bmatrix} H_A(x) \\ H_B(x) \\ H_C(x) \\ \end{bmatrix}
Written by@[Minsu Kim]
🌈22살 대학생 학생 개발자🙂