Minsu's Dev Log

Linear Regression의 cost 최소화 알고리즘의 원리

January 02, 2019

해당 게시물은 Edwith에서 제공하는
머신러닝과 딥러닝 BASIC을 듣고 요약 정리한 글입니다.

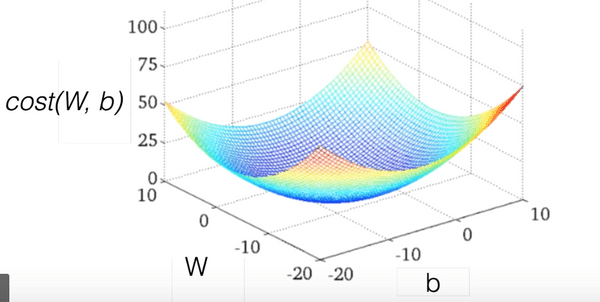
Hypothesis and Cost

H(x)=Wx+bH(x) = Wx + b cost(W,b)=1m∑_i=1m(H(x(i))−y(i))2cost(W,b) = \dfrac{1}{m}\sum\_{i=1}^m(H(x^{(i)}) - y^{(i)})^2

Simplified hypothesis

H(x)=WxH(x) = Wx cost(W)=1m∑_i=1m(Wx(i)−y(i))2cost(W) = \dfrac{1}{m}\sum\_{i=1}^m(Wx^{(i)} - y^{(i)})^2

What cost(W) looks like?

X Y
1 1
2 2
3 3

W = 1, cost(W) = ?

Cost(W)=(11−1)2+(12−2)2+(1∗3−3)=0Cost(W) = (1 _ 1 - 1)^2 + (1 _ 2 - 2)^2 + (1 * 3 - 3) = 0

W = 0, cost(W) = 4.67

Cost(W)=13((01−1)2+(02−2)2+(0∗3−3)2)=4.67Cost(W) = \dfrac{1}{3}((0 _ 1 - 1)^2 + (0 _ 2 - 2)^2 + (0 * 3 - 3)^2) = 4.67

W = 2, cost(W) = 4.67

Cost(W)=13((21−1)2+(22−2)2+(2∗3−3)2)=4.67Cost(W) = \dfrac{1}{3}((2 _ 1 - 1)^2 + (2 _ 2 - 2)^2 + (2 * 3 - 3)^2) = 4.67

W값의 변화에 따라 달라지는 cost(W)의 값 그래프

1

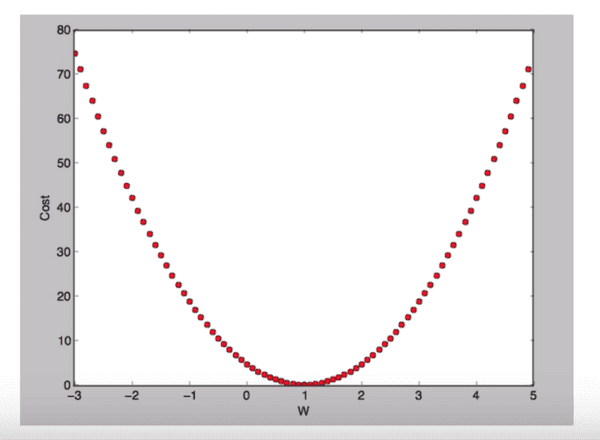
우리의 목표 : cost(W)가 최소화 되는 점을 찾는 것

Gradient descent algorithm

  • 경사하강법
  • cost(W)의 최솟값을 찾는데 사용
  • 아무 지점에서나 시작 가능
  • W의 값을 조금씩 줄이며 cost(W)의 값을 계산
  • 반복적인 작업
  • 경사도를 구하는 법 : 미분

Formal definition

cost(W,b)=12m∑_i=1m(H(x(i))−y(i))2cost(W,b) = \dfrac{1}{2m}\sum\_{i=1}^m(H(x^{(i)}) - y^{(i)})^2 W:=W−aaaWcost(W)W := W - a\dfrac{a}{aW}cost(W) \\

미분 과정

1.

W:=W−aaaW12m∑_i=1m(Wx(i)−y(i))2W := W - a\dfrac{a}{aW}\dfrac{1}{2m}\sum\_{i=1}^m(Wx^{(i)} - y^{(i)})^2

2.

W:=W−a12m∑_i=1m2(Wx(i)−y(i))x(i)W := W - a\dfrac{1}{2m}\sum\_{i=1}^m2(Wx^{(i)} - y^{(i)})x^{(i)}

3.

W:=W−a1m∑_i=1m(Wx(i)−y(i))x(i)W := W - a\dfrac{1}{m}\sum\_{i=1}^m(Wx^{(i)} - y^{(i)})x^{(i)}

Convex function

  • 경사하강법을 사용할 때 그래프가 아래와 같은 모양인지 확인 필수
2
Written by@Minsu Kim
Software Engineer at KakaoPay Corp.