BOJ 2263 트리의 순회
December 05, 2018
트리의 순회
| 시간 제한 | 메모리 제한 |
|---|---|
| 5초 | 128MB |
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다.
이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때,
프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다.
다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고,
그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
예제 입력
3
1 2 3
1 3 2예제 출력
2 1 3풀이
백준의 예제는 너무 쉽게 끝나므로 다음의 예로 설명하겠습니다.
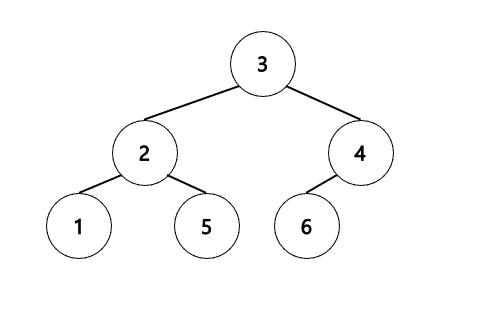
Inorder Traversal
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 2 | 5 | 3 | 6 | 4 |
Postorder Traversal
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 5 | 2 | 6 | 4 | 3 |
Preorder Traversal
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 3 | 2 | 1 | 5 | 4 | 6 |
접근 방법
후위 순회의 마지막 출력은 루트 노드다.
전체 배열 0 ~ 5 번쨰의 5번째의 3은 전체 트리의 루트 노드
왼쪽 서브 트리 0 ~ 2 번째의 2번째의 2는 왼쪽 서브트리의 루트노드
오른쪽 서브 트리 3 ~ 4 번째의 4번째의 4는 오른쪽 서브트리의 루트노드
root = postorder[postorder_end]왼쪽 서브 트리의 사이즈는 다음의 공식으로 얻을 수 있다.
- (중위 순회 루트 노드의 순회 순서) - (중위 순회의 시작 인덱스)
오른쪽 서브 트리의 사이즈는 자연스럽게 얻을 수 있다.
- (원본 트리 사이즈) - (왼쪽 서브 트리 사이즈) - 1
inorder_root = inposition[root]
left_size = inorder_root - inorder_start따라서 중위 순회의 루트 노드 인덱스를 기준으로 리스트의 왼쪽은
왼쪽 서브 트리가 되고 리스트의 오른쪽은 오른쪽 서브트리가 된다.
이를 위해서 중위 순회의 순회 순서인 inposition 배열을 하나 만들어야 한다.
inposition = [0] * (max(inorder) + 1)
for i, v in enumerate(inorder):
inposition[v] = i따라서 다음과 같은 inposition 리스트가 하나 생성될 것이다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 3 | 5 | 2 | 4 |
이제 본격적으로 함수를 구현해볼 차례다.
함수의 정의
- inorder_start : 중위 순회 시작 인덱스
- inorder_end : 중위 순회 마지막 인덱스
- postorder_start : 후위 순회 시작 인덱스
- postorder_end : 후위 순회 마지막 인덱스
def get_preorder(inorder_start, inorder_end, postorder_start, postorder_end):해당 함수를 재귀적으로 호출하면서 왼쪽 서브트리, 오른쪽 서브트리
순서로 방문하면서 루트 노드를 출력해주면 된다.
간단한 흐름 설명
루트 노드
- root = postorder[postorder_end] = 3
- print(root, end=” ”) 3 출력
- inorder_root = inposition[root] = 3
- leftsize = (inorderroot - inorder_start) = (3 - 0) = 3
| index | 3 | index | 5 |
|---|---|---|---|
| inorder | 3 | postorder | 3 |
- 중위 순회의 중간 인덱스와 후위 순회의 마지막 인덱스가 루트 노드
왼쪽 서브 트리
- inorder_start : 0
- inorderend : (inorderroot - 1) = 2
- postorder_start : 0
- postorderend : (postorderstart + left_size - 1) = 2
| index | 0 | 1 | 2 | index | 0 | 1 | 2 |
|---|---|---|---|---|---|---|---|
| inorder | 1 | 2 | 5 | postorder | 1 | 5 | 2 |
- 왼쪽 서브 트리의 postorder_end번째 노드(2)가 새로운 루트 노드
오른쪽 서브 트리
- inorderstart : (inorderroot + 1) = 4
- inorder_end : 5
- postorderstart : (postorderstart + left_size) = 3
- postorderend : (postorderend - 1) = 4
| index | 4 | 5 | index | 3 | 4 |
|---|---|---|---|---|---|
| inorder | 6 | 4 | postorder | 6 | 4 |
- 오른쪽 서브 트리의 postorder_end번째 노드(4)가 새로운 루트 노드
다음과 같은 과정을 재귀적으로 호출하면 문제가 해결된다.
탈출 조건
postorder_start > postorder_endinorder_start > inorder_end
함수 구현부
def get_preorder(inorder_start, inorder_end, postorder_start, postorder_end):
if postorder_start > postorder_end:
return
if inorder_start > inorder_end:
return
root = postorder[postorder_end]
print(root, end=" ")
inorder_root = inposition[root]
left_size = inorder_root - inorder_start
get_preorder(inorder_start, inorder_root - 1,
postorder_start, postorder_start + left_size - 1)
get_preorder(inorder_root + 1, inorder_end,
postorder_start + left_size, postorder_end - 1)메인 함수 부분
import sys
sys.recursionlimit(10 ** 6)
n = int(sys.stdin.readline())
inorder = list(map(int, sys.stdin.readline().split(' ')))
postorder = list(map(int, sys.stdin.readline().split(' ')))
inposition = [0] * (max(inorder) + 1)
for i, v in enumerate(inorder):
inposition[v] = i
get_preorder(0, n - 1, 0, n - 1)결과(Preorder Traversal)

3 ❯ 2 ❯ 1 ❯ 5 ❯ 4 ❯ 6 의 순서로 출력이 된다.
코드를 보기만 하는 것 보다 직접 진행 순서를 한 번씩
그려보면서 이해해보는 것이 좋을 것이다😁😁.
✅ 코드는 [여기]에서 확인할 수 있다.
재귀 함수를 사용한 풀이 방법이라 속도가 좋지않다.
시간 초과가 생긴다면 PyPy3로 제출해 보길 바란다.
